Newton's Laws

CSEC Physics Syllabus - Effective for examinations from May - June 2015

Section A - Mechanics

Dynamics: Motion in a Straight Line

Newton's Laws

Specific Objective 4.4

state Newton's three laws of motion;

Specific Objective 4.5

use Newton's laws to explain dynamic systems;

Pixabay

Newton's First Law

An object at rest will stay at rest and a moving object will continue to move with uniform velocity unless acted on by an external force.

 

Uniform Velocity = Constant Speed in a Straight Line

Newton's Second Law

The force applied to an object is directly proportional to the object's acceleration. 

Force α Acceleration

Force = k × Acceleration, where k is a constant

⸫ Force = Mass × Acceleration

Newton's Third Law

For every action force acting on one object, there is an equal and opposite reaction force acting on another object. 

Example 1

a)    If a force of 240 N is applied to an object of mass 8 kg and no frictional forces are opposing the motion, calculate its acceleration.

b)    If the object starts from rest, find its velocity after 4 s.

    Solution

a)    To calculate the acceleration of the object, we use Newton's second law 

N.B. There are no frictional forces opposing the force applied to the object causing the motion and the resulting acceleration 

Force = Mass × Acceleration

240 N = 8 kg × Acceleration

 Acceleration = 240 N ÷ 8 kg

⸫ Acceleration = 30 N/kg or 30 m/s²

b)    The velocity of the object after 4 s is determined using the following formula:

Final Velocity, v = Initial Velocity, u + (Acceleration, a × Time, t)

v = u + at

Where,

v = ? (what we want to find) 

u = 0 (the object starts from rest)

a = 30 m/s²

t = 4 s

v = 0 + (30 m/s² × 4 s)

v = 120 m/s

Example 2

Calculate the force needed to give a mass of 5 kg an acceleration of:

a)    2 m/s²

b)    10 cm/s²

c)    5 km/s²

    Solution

a)    Using Newton's second law

Force = Mass × Acceleration

Force = 5 kg × 2 m/s²

⸫ Force = 10 N or 10 kgm/s²

b)    Using Newton's second law

Force = Mass × Acceleration

Force = 5 kg × 10 cm/s²

We must convert the acceleration from 10 cm/s² to m/s²

Recall, centi (c) is equivalent to 0.01 

Force = 5 kg × [10 × (0.01)] m/s²

Force = 5 kg × 0.1 m/s²

⸫ Force = 0.5 N

c)    Using Newton's second law

Force = Mass × Acceleration

Force = 5 kg × 5 km/s²

We must convert the acceleration from 5 km/s² to m/s²

Recall, kilo (k) is equivalent to 1 000

Force = 5 kg × [5 × (1 000)] m/s²

Force = 5 kg × 5 000 m/s²

⸫ Force = 25 000 N

Example 3

A force of 12 N is used to move a box of mass 20 kg along the ground. If there is a constant frictional force of 4.0 N opposing the motion, what will be the acceleration of the box?

    Solution

Using Newton's second law:

Force = Mass × Acceleration

Resultant Force =  Mass × Acceleration

To determine the Resultant force we must Resolve the forces Horizontally:

12 N - 4 N =  20 kg × Acceleration

8 N =  20 kg × Acceleration

Acceleration = 8 N ÷ 20 kg

⸫ Acceleration = 0.4 m/s²

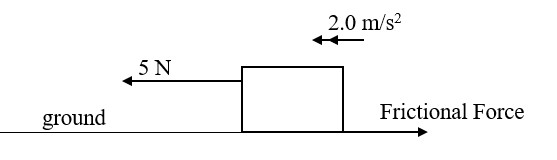
Example 4

A trolley of mass 1.5 kg is pulled by an elastic cord and is given an acceleration of 2.0 m/s². Find the frictional force acting on the trolley if the tension in the elastic cord is 5 N.

    Solution

Using Newton's second law:

Force = Mass × Acceleration

Resultant Force =  Mass × Acceleration

To determine the Resultant force we must Resolve the forces Horizontally:

5 N - Frictional Force =  1.5 kg × 2.0 m/s²

5 N - Frictional Force =  3 N

Frictional Force  = 5 N - 3 N

⸫ Frictional Force = 2 N