Vector Perpendicular & Parallel Components

CSEC Physics Syllabus - Effective for examinations from May - June 2015

Section A - Mechanics

Vectors

Specific Objective 2.4

explain that a single vector is equivalent to two other vectors at right angles.

Pixabay

Perpendicular and Parallel Components 

Every vector can be represented by two separate vectors called perpendicular and parallel components.

Consider the following arbitrary vector:

This vector can be represented by two vectors which are perpendicular to each other and called Perpendicular (to the horizontal) and Parallel (to the horizontal) components of the vector. We leave out the 'to the horizontal' because it is implied. Similarly, the 'to the horizontal' could be 'to the vertical'. These lines exist to give context to the angle of action of the vector.

How is this done?

Step 1:

We form a parallelogram using the arbitrary vector as a diagonal as shown in Figure 1 below. I deliberately used red and blue coloured lines to represent the horizontal and the vertical sides of the parallelogram respectively. 

Figure 1

Step 2: 

In Figure 1 above, moving from A to B to C is equivalent to moving from A to C, using vector theory. We can therefore replace lines AB and BC with vectors as seen in Figure 2. We can see that vector AB is a horizontal vector and vector BC is a perpendicular vector which is perpendicular to vector AB.

Figure 2

3. If we separate vectors AC and the combination of AB and BC, we get:

Figure 3

4. Translating vector BC along vector AB such that the two vectors start at a common point, we get:

Figure 4

It can be seen in Figure 4, vectors AB and BC are the parallel and perpendicular components of vector AC respectively. Remember we are speaking with respect to the horizontal (which is an imaginary line, used as a reference).

This analysis shows that any vector could be replaced with two vectors which are perpendicular to each other. This vectors are called Perpendicular and Parallel components of the vector. 

Mathematically, we can calculate the value of these components.

How is this done?

With the use of Figure 2, if we know the angle between vectors AB and AC as seen in Figure 5 below; using Trigonometric ratios then we can calculate the perpendicular (vector BC) and parallel (vector AB) components of vector AC.

Figure 5

Trigonometric Ratios:

There are many ways to remember these ratios. My favorite two are SOHCAHTOA, pronounced (so-ca-toe-ah) and Some Old Horses Can Always Hear Their Owners Approach. 

Therefore, using the ratios we get:

Example 1:

A force of 50 N acting at 25° to the horizontal, is used to pull a box along a smooth (frictionless) horizontal surface as shown in Figure 6 below. Calculate the perpendicular (vertical) and parallel (horizontal) components of this pulling force. 

Figure 6

Solution:

Figure 7

Perpendicular Component = 50 N ✕ sin (25°)
∴ Perpendicular Component = 21.1 N (3 sig. fig.)

Parallel Component = 50 N ✕ cos (25°)

∴ Parallel Component = 45.3 N (3 sig. fig.)

Example 2

A ball is stuck with a force 120 N at an angle of 45° to the horizontal as seen in Figure 8 below. Calculate the perpendicular (vertical) and parallel (horizontal) components of the 120 N force.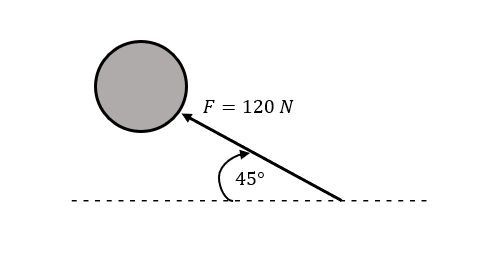

Figure 8

Solution:

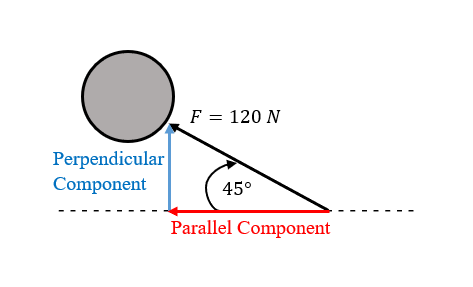Figure 9

Perpendicular Component = 120 N ✕ sin (45°)
∴ Perpendicular Component = 84.9 N (3 sig. fig.)

Parallel Component = 120 N ✕ cos (45°)

∴ Parallel Component = 84.9 N (3 sig. fig.)

Notice that at an angle of 45°, both the perpendicular and parallel components have the same magnitude (value). 

Example 3:

A ferry transporting passengers from Saint Lucia to Dominica is moving at 24.8 ms^-1 at an angle of  22.7° to the vertical (an imaginary straight line from north to south). Calculate the perpendicular (vertical) and parallel (horizontal) components of this velocity vector. 

Solution:

Figure 10

Perpendicular Component = 24.8 ms^-1 ✕ sin (22.7°)
∴ Perpendicular Component = 9.57 ms^-1 (3 sig. fig.)

Parallel Component = 24.8 ms^-1 ✕ cos (22.7°)

∴ Parallel Component = 22.9 ms^-1 (3 sig. fig.)