CSEC Physics Syllabus - Effective for examinations from May - June 2015
Section A - Mechanics
Statics
Turning Forces
Turning Forces
Specific Objective 3.8
define the moment of a force, T;
Specific Objective 3.9
apply the principle of moments;
 |
| Pixabay |
Moment of a Force
The moment of a Force is calculated by multiplying the force acting, F by the perpendicular distance, d from the line of action of the force to the pivot.
 |
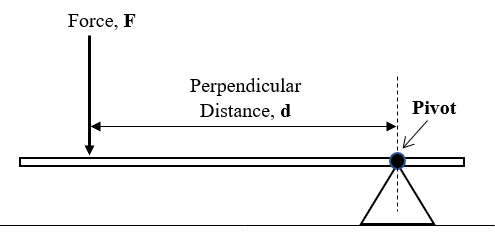| Diagram 1 |
Symbol:
Moment of a Force, T.S.I. Unit:
Newton-meter, Nm.Formula:
Moment of a Force = Force × Perpendicular Distance
T = F × d
Moments could either be: Clockwise or Anti-clockwise
Clockwise Moments
A moment is considered clockwise if the force acting causes a clockwise rotation about the pivot.
 |
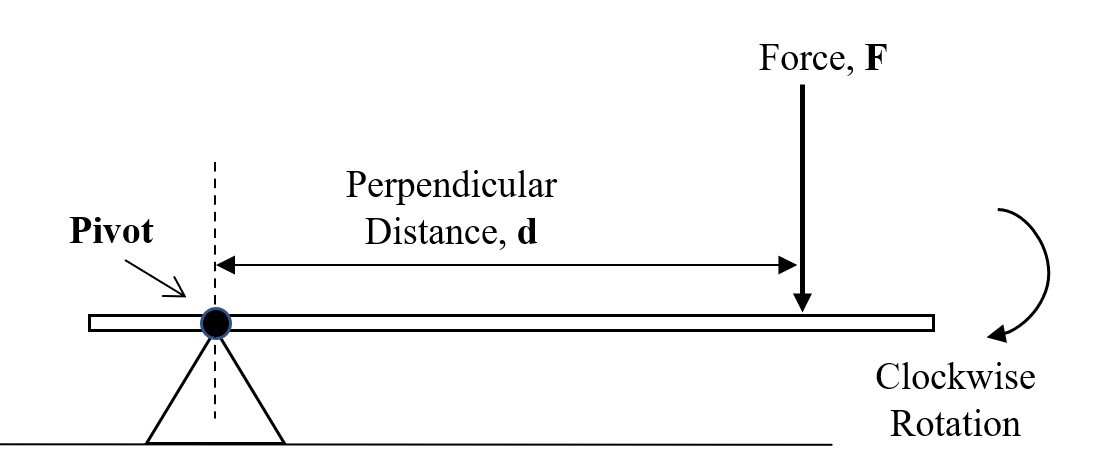| Diagram 2 |
Anti-clockwise Moments
A moment is considered anti-clockwise if the force acting causes an anti-clockwise rotation about the pivot.
 |
| Diagram 3 |
Principle of Moments
For systems in equilibrium, the sum of the Clockwise Moments about a pivot is equal to the sum of the Anti-clockwise Moments about the same pivot.
Formula:
Sum of the Clockwise Moments = Sum of the Anti-clockwise Moments
Given Clockwise Moments: T1, T2, T3
Given Anti-clockwise Moments: T4, T5, T6
T1 + T2 + T3 = T4 + T5 + T6
Example 1
The security boom is counter-balanced by a weight W, to make it easier to raise the boom. The weight of the boom is 300 N.
a) What size of counterweight, W, balances the boom?
b) What reaction force is provided by the support?
Solution
a) Using the Principle of Moments when the system is balanced:
Anti-clockwise Moment = Clockwise Moment
W × 0.5 m = 300 N × 3.0 m
W × 0.5 m = 900 Nm
W = 900 Nm ÷ 0.5 m
⸫ W = 1800 N
b) We find the Reaction Force by Resolving the Forces vertically:
Reaction Force = W + 300 N
Reaction Force = 1800 N + 300 N
⸫ Reaction Force = 2100 N
Example 2
In the figure below, AC represents a trapdoor of width 100 cm which is hinged at A. The weight of the trapdoor is 30 N and its centre of gravity is 50 cm from A. An object is placed on the so that its weight of 40 N acts through B, which is 25 cm from A.
a) Redraw the diagram and show the two forces and add a third force applied vertically at C, which just lifts the door.
b) Calculate the magnitude of this force at C.
Solution
b) Using the Principle of Moments when the system is balanced:
Clockwise Moment = The Sum of the Anti-clockwise Moments
F × 100 cm = (40 N × 25 cm) + (30 N × 50 cm)
F × 1.0 m = (40 N × 0.25 m) + (30 N × 0.50 m)
F × 1.0 m = 10 Nm + 15 Nm
F × 1.0 m = 25 Nm
F = 25 Nm ÷ 1.0 m
⸫ F = 25 N
Example 3
The figure below shows a tray held horizontally by one hand at its edge. The tray has a weight of 5.0 N. The hand supports the tray with a downward force F from the thumb and an upward normal reaction force N from the fingers. These two forces are 5.0 cm apart. A glass of water of weight 2.0 N is supported by the tray at a distance of 30 cm from the normal reaction N where the balanced tray is pivoted.
Calculate:
a) The magnitude of the force, F provided by the thumb.
b) The magnitude of the reaction force, N.
Solution
a) Using the Principle of Moments when the system is balanced:
Anti-clockwise Moment = The Sum of the Clockwise Moments
F × 5 cm = (5 N × [20 cm - 5 cm]) + (2 N × 30 cm)
N has no moment because its perpendicular distance = 0
F × 5 cm = (5 N × 15 cm) + (2 N × 30 cm)
F × 0.05 m = (5 N × 0.15 m) + (2 N × 0.30 m)
F × 0.05 m = 0.75 Nm + 0.6 Nm
F × 0.05 m = 1.35 Nm
F = 1.35 Nm ÷ 0.05 m
⸫ F = 27 N
b) The magnitude of the reaction force, N is found by Resolving the Forces vertically:
N = F + 5 N + 2 N
N = 27 N + 5 N + 2 N
⸫ N = 34 N
0 Comments